Backtracking algorithms are very powerful, and are often the keystone in a successful combinatorial search algorithm. They can allow us to proceed in finding complex solutions where other algorithms fall far short of the mark.

Many famous problems in computer science can be solved using backtracking, including: The Eight Queens Problem, The Sudoku Puzzle, The Graph Coloring Problem, and The Knapsack Problem.

This article will explore the ideas of combinatorial search and backtracking within the context of a classical chess problem: The Eight Queens Problem.

The Eight Queens Problem

If you are unfamiliar with the rules of chess, or the Eight Queens problem, you will want to read this.

The Eight Queens Problem asks us, "How many ways can we position eight queens on a chessboard such that no queen threatens another?"

A chessboard is an 8x8 grid, and the queen is a powerful piece, capable of attacking any square on her row, column, or diagonal. For the visually inclined, that looks like this:

In chess, a piece threatens another piece if it is able to capture the other in a single move. In the above picture, the two queens are not threatening one another.

Stated formally, the problem has two rules for a successful candidate:

1. There must be 8 queens on the board

2. No queen threatens another

Then, we are to count the number of successful candidates.

Wait, but why do we need backtracking at all? Could we not solve this problem using some other algorithm?

Let's take a deeper look at the problem.

Analyzing the Problem

Let's analyze the problem a bit. First, let us relax the constraints a bit and ask ourselves, "How many ways could we arrange eight queens on the board?"

This is a simpler problem, with a much clearer answer: We have 64 squares, and need to place 8 pieces. Since every piece is a queen, the order does not matter. And since the order doesn't matter, it comes down to a very common problem in computer science: n choose k.

n choose k is way of calculating how many combinations we can create when the number of things to choose from is greater than or equal to the number of things chosen.

In our case, we have 64 choose 8 possible combinations, which is equal to:

$$\frac{64!}{8!(64-8)!} = 4,426,165,368$$

That's a lot of different ways we could arrange eight queens on a chess board. However, we should be thankful that the order doesn't matter. For instance, if we were placing 8 different pieces on on a chessboard, we'd be looking at a very large number of permutations:

$$\frac{64!}{(64-8)!} = 178,462,990,000,000$$

Yep, that's 178 trillion.

These numbers are a challenge even to modern computers, and they indicate that a simple brute force algorithm will not work.

Since we are searching for specific combinations that fit a certain constraint (no queen threatens another), this is a combinatorial search problem. Fortunately, we can use the constraints of the problem against it - by backtracking.

The Essence of Backtracking

Enter backtracking.

In a single sentence, backtracking is recognizing when a partial candidate has failed to meet the constraints of the problem, and turning the F around.

But let's get a little more in depth than that.

The thing that really helped backtracking click for me was visualizing the path from the empty board to any one of the solutions as a tree.

Let us start with the root of this tree: The empty chessboard. From the empty board, we can place a single queen, and since the board is empty we can choose any of the 64 squares, like so:

By adding a piece to the board, we can visualize that we are descending lower into the tree.

So, we have 64 possible first moves. What about second moves? Naturally, the second comes after the first, and we can't place a piece on an occupied square, so we have one less square to choose from. Therefore, from any of the 64 first moves, we can make 63 possible second moves.

Already it is difficult to show a tree that demonstrates all of the possible second moves. Instead, I'm going to zoom in on a specific part of that tree, so that we can make two critical observations that will help us write a correct algorithm:

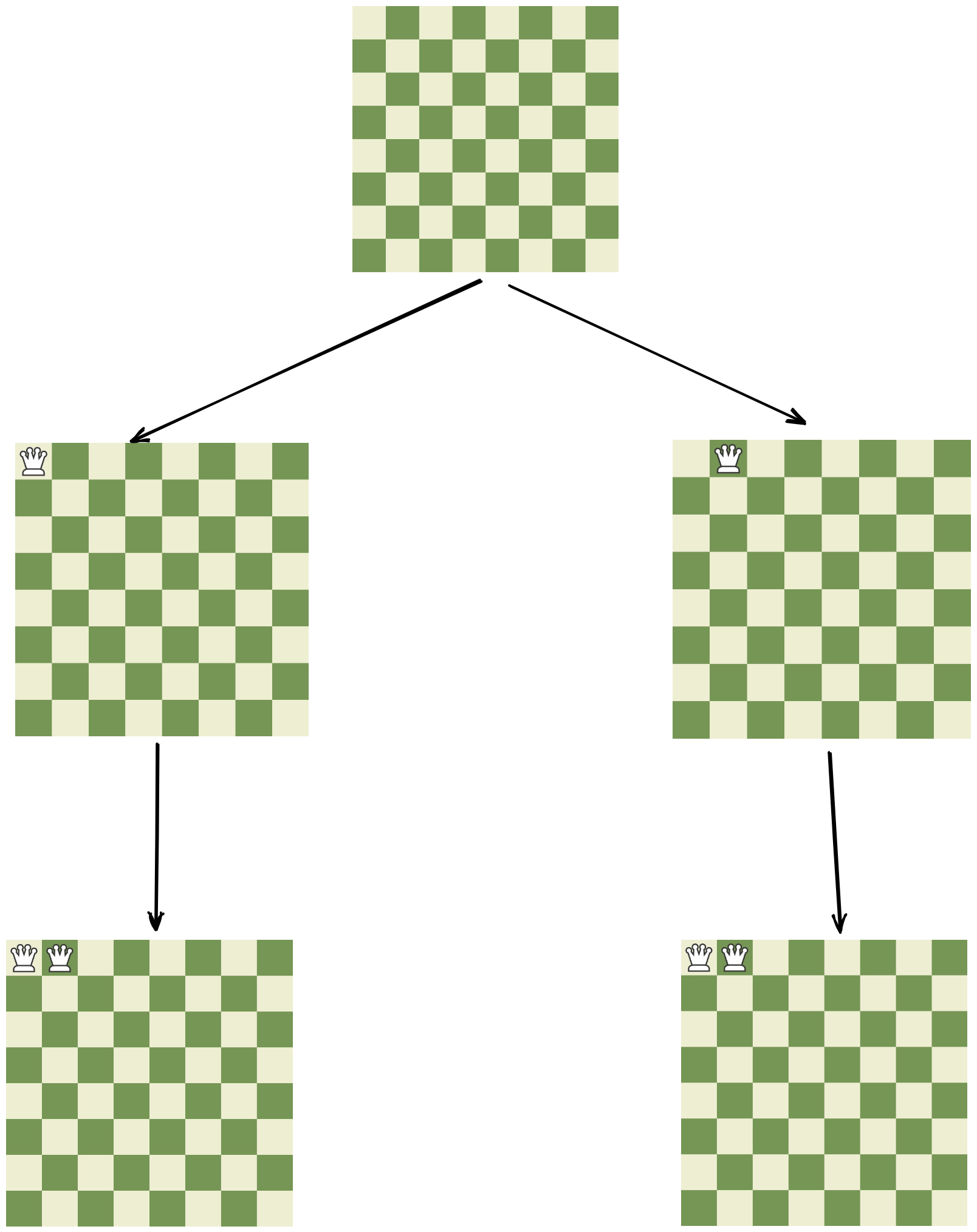
So, we've made our first and second moves. But wait! Something is going on here!

1. We've just created the same combination! Since all queens are the same, there is no difference between these two board states. This is critical. We must make sure our algorithm does not revisit previously encountered board states. If we fail to do this, our tree goes from 4.4 billion to 172 trillion board states in size! Bad!

2. Both of these also wrong! These queens are threatening each other! Even if we create an algorithm that weeds out duplicate combinations, we can see that there is no point in adding another piece if our last move fails to meet the constraints of the problem.

Point 2 is the very essence of backtracking. We need to use the constraints of the problem to reject bad moves while we descend into the tree (by adding pieces), not after we've picked all 8 positions!

If we reject the board state in the case shown above, we will have effectively pruned 62 choose 6 incorrect board states from the search tree:

$$\frac{62!}{6!(62-6)!} = 61,474,519$$

That is 61.4 million bad decisions gone in the blink of an eye. If only I had this kind of power in real life.

These savings add up fast. In the end, they are what makes a backtracking solution superior to a naive brute force solution.

In summary, we need an algorithm that finds the set of appropriate next moves for a given board state, and rejects the moves that fail to meet the problem constraints immediately. Additionally, we must skip board states that have already been encountered.

Wow, sounds cool, but how do we write such legendary code? Well...

How to Write a Backtracking Algorithm

This is the section where we will begin looking at some code. I'm not cool, so I'm going to write the code in C, like a crusty dinosaur. Keep in mind the techniques used here work for any language.

The tree described in the previous section is a recursive data structure, and therefore the backtracking algorithm is a recursive algorithm. It is effectively a variant of depth-first search, but it does have a few more moving parts.

Take a read through these function signatures, and then we'll talk about them:

void backtrack(state_t *p);
int  reject(state_t *p);
int  accept(state_t *p);

Let's go through these in the general sense. backtrack is the main function here. It is responsible for calling both reject and accept, both of which are predicate functions that return true or false (or in C, non-zero or zero). Additionally, backtrack has the responsibility of iterating through the available next moves, and calling itself for each one.

reject returns true if the board state fails to meet the constraints of the problem. This is pretty important for the turning the fuck around part of backtracking.

accept returns true if the board state has met the acceptance criteria. You'll see that this function doesn't actually have much to do, since it gets called after reject.

Optionally, you may wish to write routines for finding the set of possible next moves, making a move, and undoing a move. That's largely dependent on the complexity of the problem at hand. I left them out because a chess board is just an 8x8 grid, so it was easy enough solve this problem by looping through the rows and columns.

Moving on, let's take a quick look at one possible way to model the Eight Queens problem: a stack!

typedef struct move_t {
    int rank; // chess lingo for "row"
    int file; // chess lingo for "column"
} move_t;

typedef struct state_t {
    move_t moves[DEPTH]; // a stack of moves, DEPTH = 8
    int len; // the stack index & array len
} state_t;

I found it easy enough to model the board state as a stack of moves. Doing so makes it quite efficient for making a move (pushing to the stack), and undoing a move (popping off the stack).

At any given recursion into backtrack, our reject predicate just needs to check the validity of the newest move against the previous moves, which amounts to iterating an array of grid coordinates of size 8. accept only needs to check the size of the stack!

Let's look at the full code:

typedef struct move_t {
    int rank; // chess lingo for "row"
    int file; // chess lingo for "column"
} move_t;

typedef struct state_t {
    move_t moves[DEPTH]; // a stack of moves, DEPTH = 8
    int len; // the stack index & array len
} state_t;

void backtrack(state_t *p);
int  reject(state_t *p);
int  accept(state_t *p);
int  threatens(move_t *x, move_t *y); // helper for reject

void backtrack(state_t *p) {
    if (reject(p)) {
        return;
    }

    if (accept(p)) {
        /* you win, do something awesome */
        return;
    }

    /* if a move has been made, next move should skip 
       to the rank after, as this prevents revisiting 
       previous board states */
    for (int rank = p->len ? p->positions[p->len - 1].rank + 1 : 0;
         rank < RANKS; ++rank) {
        for (int file = 0; file < FILES; ++file) {

            /* push next move to the stack */
            p->moves[p->len++] =
                (move_t){.rank = rank, .file = file};

            backtrack(p);

            /* pop last move off the stack */
            --p->len;
        }
    }
}

int reject(state_t *p) {
    /* impossible to fail if less than 2 moves */
    if (p->len < 2) {
        return 0;
    }

    /* test newest move against previous moves */
    move_t *new_move = &p->positions[p->len - 1];
    for (move_t *previous_move = p->positions;
         previous_move != new_move; ++previous_move) {

        if (threatens(new_move, previous_move)) {
            return 1;
        }
    }

    return 0;
}

/* since this is called after reject, we can simply return
   true if the size of the stack has reached DEPTH */
int accept(state_t *p) {
    return p->len == DEPTH;
}

int threatens(move_t *x, move_t *y) {
    return x->file == y->file || x->rank == y->rank ||
           abs(x->file - y->file) == abs(x->rank - y->rank);
}

All right, recursive stuff can be a lot to take in, but the main take away here is the relationship that backtrack has with reject, accept, and itself. Here's a breakdown of the important parts:

1. We have a rejection policy. Remember, this is the thing that is capable of pruning millions of bad paths out of our search tree!

2. We iterate the set of next possible moves at each level of the tree. As I mentioned briefly before, some problems may lend themselves to making separate routines for this. However, the chess board is actually linear enough that I felt row-major looping was sufficient.

3. We don't revisit previously seen board states. The clever trick here is that you should always position new moves after the last played move. For problems other than this, you may need to use a hash set or something like that.

Summary

All right, at this point you might be wondering, "What the hell is the actual answer to the Eight Queens problem? I can't believe I read all that garbage code not to find out at the end! ARRRGGGGGHHH!!!"

Well, the bad news is that if you don't know, I'm not going to spoil it for you. Please don't hulk out on me. Instead, write some code and run it.

Backtracking is a very powerful technique, and the key take away is this: If the problem constraints allow you to know whether a partial candidate has failed, use it to your advantage!

Many problems can be solved with backtracking. I hope this article helped you in understanding backtracking well enough that you feel prepared to have a go at something a bit more exciting than the Eight Queens Problem.

Why don't you try your hand at writing a Sudoku solver?

Thanks for reading!

Further Reading

The pseudocode section of the backtracking wiki helped me understand the structure and relationships of these functions a great deal, and basically served as my primary reference for the structure of the above code. Definitely worth a read.